

Sometimes this expression is written as 2πr(r + h) in certain geometry texts. Those values are πr 2 + πr 2 + 2πrh = 2πr 2 + 2πrh. The top, the bottom, and the walls of the cylinder (the lateral surface area) determine the total surface area.
So, the area of the rectangle is A = l x w = C x h = 2πr x h = 2πrh.įinally, if we put all the three surfaces together, we can arrive at the formula for the complete surface area of a cylinder. The dimensions of the rectangle are the circumference, C = 2πr, and the height of the cylinder, h. When the cylinder wall is completely open, we see that the circumference of the circle becomes the length of the final rectangle. The circumference has been marked in red. We know that the distance around a circle is called its circumference, C = 2πr. The top of the original cylinder is a circle. But we need to go back to the original cylinder for a moment before we calculate the rectangle's area. Fortunately, the area of a rectangle is easy to calculate. When the cylinder's wall is completely open, it takes the form a very recognizable, basic shape. Almost like opening double doors to a fancy home, the walls spread apart. Now, from the newly cut edge, the cylinder wall will be spread open. See the dashed segment in step one of the diagram to the right. From the bottom to the top of the can, a cut is made. Imagine starting with a cylinder, like a typical can, and then cutting the can up its wall.
We can manipulate the curved wall of a cylinder to produce a recognizable shape. The surface being referred to is the curved wall of the cylinder. The third surface, the lateral surface area, is less easy to visualize for the purposes of calculating its area, especially since it does not appear to be in a shape that fits a known area like a triangle or parallelogram.
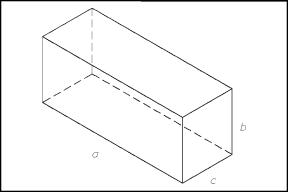
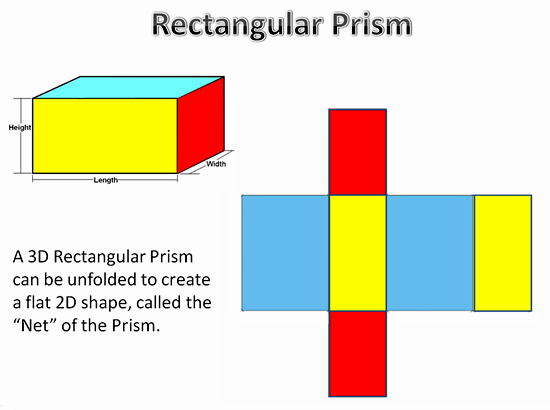
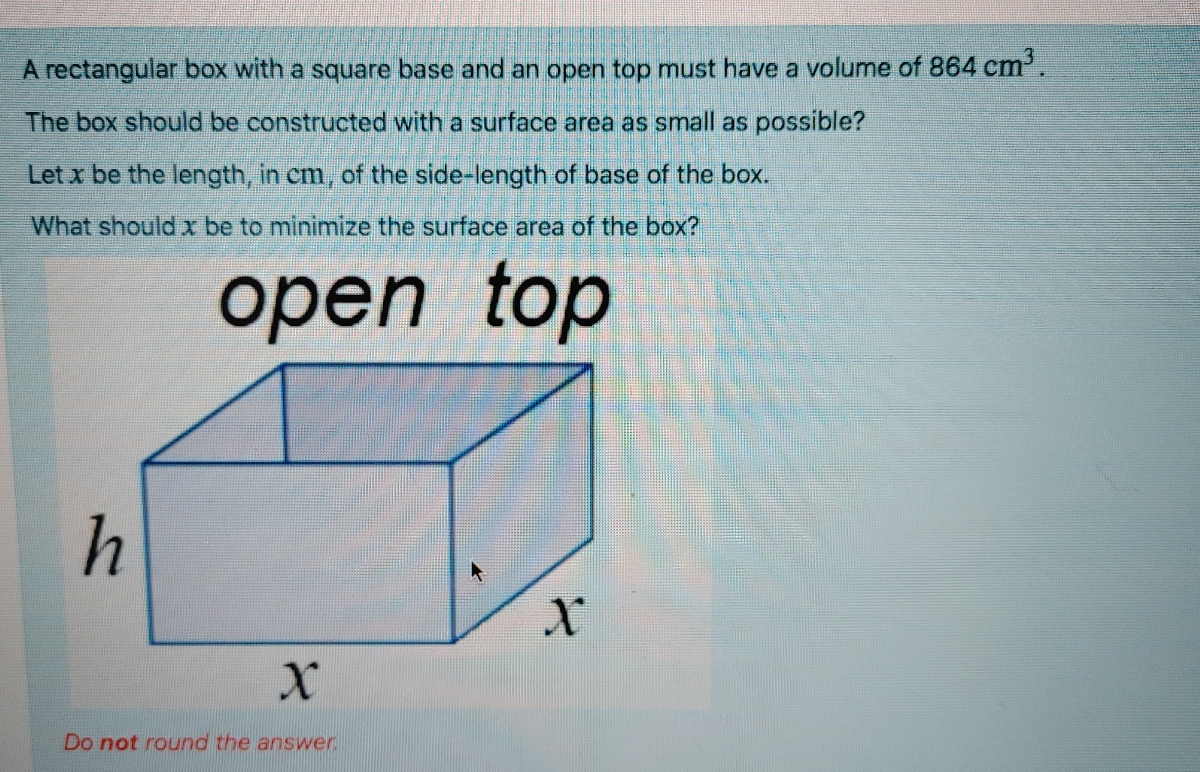
So, the area of two circles would be πr 2 + πr 2 = 2πr 2. The top and bottom, which are circles, are easy to visualize. Ideo: Surface Area of a Rectangular PrismĪ cylinder has a total of three surfaces: a top, bottom, and middle. SA = 2Įxample 2: Given l = 6 mm, w = 9 mm, and h = 8 mm, the surface area would be. Let's calculate the area of each surface.Įxample 1: Given l = 4 yds, w = 2 yds, and h = 5 yds, the surface area would be. Using the labeling of the general prism diagram above, a formula can be created for dealing with the surface area of prisms. The surface are of a prism is nothing more than the sum of all the areas of these rectangles. There is a front, back, top, bottom, left, and right to every rectangular prism. The area of rectangles have been discussed in another section, which is available for review before proceeding, if necessary.Īs the diagram below indicates, there are six surfaces to a rectangular prism. This makes calculating the areas of these surfaces very easy to do. It is also a figure most people have personal experience due to either wrapping or opening gifts.Īll the surfaces of a prism are rectangular. It is the most simple figure of all the solids. I would just like to know what equations I would need to find the surface area of the open top rectangular container.This is the best figure to begin with when investigating surface area. the cost of the material ($ per square cm).Write and test a program that asks for the following inputs, in order: To calculate the area of the container's side, you have four rectangles with length and diameter with specified height.The base is square, and each side is equal to the given diameter.The circumference of a circle = $2\pi r$.To calculate the area of the container's side, imagine unwrapping the side into a rectangle so the area of the side is the circle circumference times the container height.The area of the base is the area of a circle = $\pi r^$.I'm a computer science major, and I was asked to write a program with the following question.Ī manufacturer wishes to compare the cost of producing an open-top cylindrical container and an open-top rectangular container.


 0 kommentar(er)
0 kommentar(er)
